Effectief financieel rekenen met Excel – Deel 4: De eindwaarde respectievelijk contante waarde van één bedrag in combinatie met een regelmatige betaalreeks
Dit artikel maakt deel uit van de reeks: ‘Effectief financieel rekenen met Excel’. Lees hier:
– Het inleidende artikel
– Deel 1 – Toegang, werking en spelregels van financiële functies
– Deel 2 – De eindwaarde respectievelijk contante waarde van één bedrag of kapitaal
– Deel 3 – De eindwaarde respectievelijk contante waarde van een regelmatige betaalreeks
– Deel 4 – De eindwaarde respectievelijk contante waarde van één bedrag in combinatie met een regelmatige betaalreeks
– Deel 5 – De contante waarde van een gelijkblijvende oneindige betaalreeks
– Deel 6 – De contante waarde van een groeiende oneindige betaalreeks
Deze berekening betreft een combinatie of optelsom van het in deel 1 en deel 2 besprokene.
Onderstaand werken we twee voorbeelden uit:
• een voorbeeld voor de eindwaarde van één bedrag plus de eindwaarde van een regelmatige reeks;
en
• een voorbeeld voor de contante waarde van één bedrag plus de contante waarde van een regelmatige reeks.
Hieruit komt naar voren dat bij de Eindwaarde de functie TW en bij de Contante Waarde de functie HW dubbel ingezet dient te worden.
Voorbeeld eindwaarde
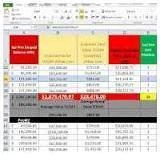
We storten op 1 januari 2013 € 30.000 bij een spaarbank tegen een intrestvergoeding van 4 % per halfjaar. Ingaande 1 juli 2013 nemen we ieder halfjaar € 1.750 van de rekening op. Over welk bedrag kunnen we u op 31 december 2026 dan nog beschikken? De laatste opname van € 1.750 vindt plaats op 1 juli 2026.
Het vraagstuk ziet er volgens het bijbehorende cashflowdiagram als volgt uit:
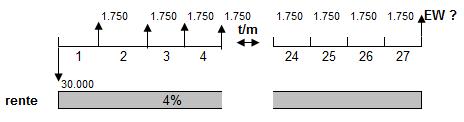
Dit voorbeeld is een combinatie van een kapitaalstorting en een regelmatige reeks opnamen (negatieve betalingen!).
We passen de basisfunctie TW dubbel toe.
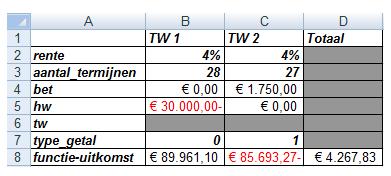
In de cellen B2:B8 is de eindwaarde berekend voor de 28 halfjaarlijkse termijnen van de kapitaalstorting (TW1 = € 89.961,10) en in de cellen C2:C8 voor de 27 halfjaarlijkse opnames (TW2 = -€ 85.693,27). De einduitkomst is gelijk aan de som van de eindwaarden: € 4.267,83 (cel D8). Hierbij wordt de reeks opnames aangemerkt als prenumerando (type_getal = 1), omdat de opnames steeds plaatsvinden aan het begin van de halfjaarlijkse perioden.
__________________________________________________________________________________
Excelleer met Excel
Werkt u regelmatig met Excel? Bent u ook veel energie kwijt aan het opstellen van analyses en presentaties? Ontdek nu de verbluffende mogelijkheden van Excel die u veel voordeel zullen opleveren, waarmee u forse tijdwinst boekt en onnodige fouten voorkomt. Benut Excel’s potentieel volledig. Volg een van de cursussen. Meld u direct aan.
__________________________________________________________________________________
Voorbeeld contante waarde
We willen de contante waarde van een dadelijk ingaande postnumerando reeks van zeven te ontvangen jaartermijnen elk groot € 2.000 bij een intrestvoet van 3 % plus één eindkapitaal na acht jaar van € 20.000 berekenen.
Het vraagstuk ziet er volgens het bijbehorende cashflowdiagram als volgt uit:
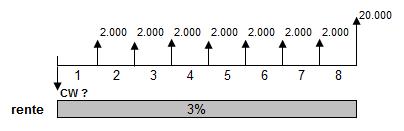
Bij de berekening van de contante waarde van één kapitaal in combinatie met een reeks gelijke betalingen maken we in Excel dubbel gebruik van de functie HW(rente;aantal-termijnen;bet;hw;type_getal).
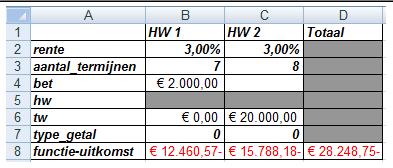
In de cellen B2:B8 is de contante waarde berekend voor de zeven termijnen (HW1 = € 12.460,57), in de cellen C2:C8 voor het eindkapitaal na acht perioden (HW2 = € 15.788,18).
De einduitkomst is gelijk aan de som van de contante waarden: € 28.248,75 (cel D8).

Geert Wessels (1957) studeerde bedrijfseconomie aan de KUB (doctoraal 1981: specialisatie ondernemingsfinanciering) en volgde daarna nog diverse postdoctorale informaticastudies. Hij heeft verschillende staf-, advies- en managementfuncties vervuld binnen met name de gezondheidszorg en de volkshuisvesting. Zijn ervaringen met Excel liggen met name op het terrein van de financiële rekenkunde.

















