Effectief financieel rekenen met Excel – Deel 2: De eindwaarde respectievelijk contante waarde van één bedrag of kapitaal
Dit artikel maakt deel uit van de reeks: ‘Effectief financieel rekenen met Excel’. Lees hier:
– Het inleidende artikel
– Deel 1 – Toegang, werking en spelregels van financiële functies
– Deel 2 – De eindwaarde respectievelijk contante waarde van één bedrag of kapitaal
– Deel 3 – De eindwaarde respectievelijk contante waarde van een regelmatige betaalreeks
– Deel 4 – De eindwaarde respectievelijk contante waarde van één bedrag in combinatie met een regelmatige betaalreeks
– Deel 5 – De contante waarde van een gelijkblijvende oneindige betaalreeks
– Deel 6 – De contante waarde van een groeiende oneindige betaalreeks
Met behulp van de functies TW en HW is het mogelijk om de eindwaarde respectievelijk de contante waarde te berekenen van één bedrag of kapitaal. Bij eindwaarde berekeningen voor één kapitaal wordt de samengestelde intrest bij de hoofdsom geteld tot het moment van uitbetaling.
Algemeen geldt hiervoor de volgende rekenregel: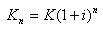
waarbij:
Kn = de eindwaarde van het kapitaal na n perioden;
K = de beginwaarde van het kapitaal in periode 0;
i = de samengestelde intrestvoet;
n = het aantal perioden.
In de financiële literatuur wordt hiervoor ook wel de ‘grote S’- schrijfwijze gebruikt: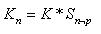
met:
p = de samengestelde intrestvoet;
n = het aantal perioden.
Contante waardeberekeningen zijn het spiegelbeeld van eindwaarde berekeningen. Bij eindwaarde berekeningen wordt van het heden naar de toekomst gerekend, bij contante waardeberekeningen van de toekomst naar het heden.
Bij contante waardeberekeningen is de vraag welk kapitaal nu op samengestelde intrest moet worden uitgezet om op termijn de beschikking te hebben over een van tevoren vastgesteld bedrag.
Bij eindwaarde berekeningen vormt Kn de onbekende grootheid, bij contante waardeberekeningen is Kn bekend en dient de parameter K berekend te worden. Na omzetting wordt de vergelijking: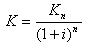
In de financiële literatuur wordt hiervoor ook wel de “grote A’-schrijfwijze gevolgd: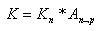
met:
p = de samengestelde intrestvoet;
n = het aantal perioden.
Voorbeeld
Een kapitaal groot € 2.000 staat gedurende acht jaar op samengestelde intrest uit à 3 % per halfjaar. Over welk eindwaarde bedrag kunnen we na het achtste jaar beschikken?
Het vraagstuk ziet er volgens het bijbehorende cashflowdiagram als volgt uit: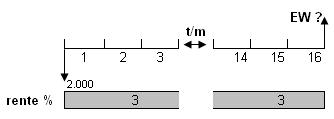
Volgens de algemene rekenregel krijgen we: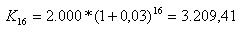
Eenzelfde uitkomst krijgen we als we de functie TW oproepen en daarbij de argumenten als volgt invoeren.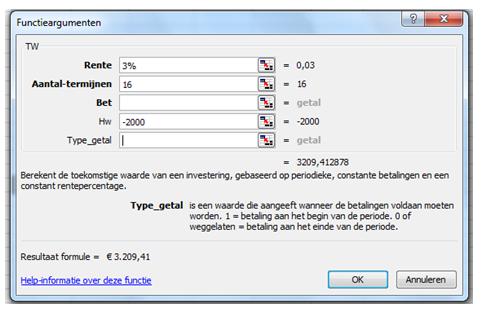
Het beginkapitaal is onder het argument Hw van een negatief teken voorzien de uiteindelijke opbrengst (TW) is, gezien vanuit van de inbrenger, positief. Voor Type_getal voeren we niets in omdat geen sprake is van een betaalreeks.
__________________________________________________________________________________
Excelleer met Excel
Werkt u regelmatig met Excel? Bent u ook veel energie kwijt aan het opstellen van analyses en presentaties? Ontdek nu de verbluffende mogelijkheden van Excel die u veel voordeel zullen opleveren, waarmee u forse tijdwinst boekt en onnodige fouten voorkomt. Benut Excel’s potentieel volledig. Volg een van de cursussen. Meld u direct aan.
__________________________________________________________________________________
Met de eindwaarde in de hand keren we nu de vraagstelling om en vragen ons af wat de hoogte van de kapitaalinbreng moet zijn om na 16 halfjaartermijnen over een bedrag van € 3.209,41 te kunnen beschikken.
Als we de verkregen eindwaarde terug vertalen naar een contante waarde berekening krijgen we: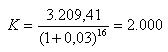
Dit is het inbrengkapitaal dat nodig is om bij 16 halfjaarlijkse perioden en een halfjaarlijkse rentevoet van 3% het eindbedrag van € 3.209,41 te bereiken. Eenzelfde uitkomst krijgen we als we de functie HW oproepen en daarbij de argumenten als volgt invoeren: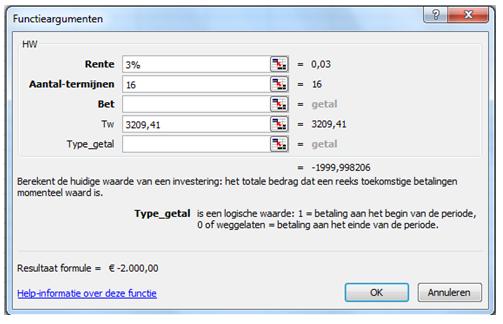
Het eindkapitaal is onder het argument TW van een positief teken voorzien, het beginkapitaal (HW) is gezien vanuit van de inbrenger negatief. Voor Type_getal voeren we niets in omdat wederom geen sprake is van een betaalreeks.
De samenhang met de andere basisfuncties
Aan de hand van het uitgewerkte voorbeeld kan – ter controle – de samenhang tussen de vijf basisfuncties getoond worden, met name in relatie tot de overige functies Rente, NPER en BET.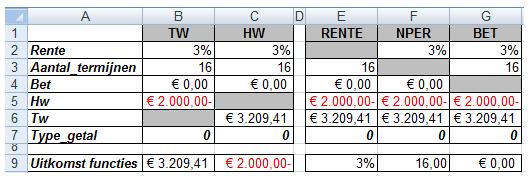
In bovenstaand cellenbereik zijn in B9 en C9 de eerder berekende resultaten weergegeven voor de functies TW en HW. De hierbij gebruikte argumenten zijn opgenomen in het bereik B2:B7 respectievelijk C2:C7.
Met de functie Rente, die opgenomen is in E9, kan berekend worden welk percentage nodig is bij de in het bereik E2:E7 opgenomen argumentwaarden. Bij deze functie dient het aantal termijnen (NPER), de huidige waarde (Hw) en de eindwaarde (Tw) ingevuld te zijn. De uitkomst is 3%.
Ter controle: dit percentage hanteerden we ook bij de berekening van TW en HW (zie de cellen B2 en C2).
Met de functie NPER, die opgenomen is in F9, kan berekend worden hoeveel termijnen nodig zijn bij de in het bereik F2:F6 opgenomen waarden. Bij deze functie dient het rentepercentage (Rente), de huidige waarde (Hw) en de eindwaarde (Tw) ingevuld te zijn. De uitkomst is 16 termijnen.
Ter controle: dit aantal termijnen hanteerden we ook bij de berekening van TW en HW (zie de cellen B3 en C3)
Met de functie BET tenslotte kunnen we de hoogte van de eventuele termijnen berekenen. Omdat we bij de berekening van de eind- en contante waarde van één kapitaal geen gebruik van maken van dit argument (zie de cellen B4 en C4) is het resultaat in G9 gelijk aan nul.
Ter controle: dit bedrag hanteerden we ook bij de berekening van TW en HW (zie de cellen B4 en C4).
In het volgende artikel uit de reeks kijken we naar de eindwaarde respectievelijk contante waarde van een regelmatige betaalreeks

Geert Wessels (1957) studeerde bedrijfseconomie aan de KUB (doctoraal 1981: specialisatie ondernemingsfinanciering) en volgde daarna nog diverse postdoctorale informaticastudies. Hij heeft verschillende staf-, advies- en managementfuncties vervuld binnen met name de gezondheidszorg en de volkshuisvesting. Zijn ervaringen met Excel liggen met name op het terrein van de financiële rekenkunde.
Klassiekers uit het archief van Financieel-Management.nl:
10 veel voorkomende fouten in Excel
10 veel voorkomende fouten in Excel – deel 2
Bekijk ook de inspirerende video’s:
Excel Video #1: Winstmaximalisatie met de oplosser
Excel Video #2: Bekijk alle opties met ‘wat-als’ analyses
Excel Video #3: Overzicht in een handomdraai met een ‘histogram’
Excel Video #4: Elimineer fouten met snijpuntoperatoren
Excel Video #5: Boek tijdswinst met draaitabellen
Excel Video #6: Foutloos vermenigvuldigen met ‘Productmat’
Excel Video #7: Effectief Formules controleren
Excel Video #8: Optimale rooster- of werkplanning
Excel Video #9: Sneller rekenen met ‘plakken speciaal’
Excel Video #10: Snel foutmeldingen opsporen en herstellen
Ontdek meer verbluffende en eenvoudige mogelijkheden van Excel:
Cursus Excel 2010
Cursus Effectieve liquiditeitsprognoses met Excel
Cursus Investeringsanalyses met Excel
Cursus VBA Excel