5 tips en tools bij maken investeringsanalyses Excel

De terugverdienperiode is wellicht de bekendste en meest gebruikte statische methode voor het beoordelen van de financiële aantrekkelijkheid van een investering. Bij een statische analyse wordt geen rekening gehouden met de tijdfactor en wordt iedere inkomende en uitgaande geldstroom gelijk gewogen in de tijd.
Word wel rekening gehouden met de tijdfactor, dan spreken we van een dynamische investeringsanalyse. Met name ter ondersteuning van dynamische investeringsanalyses is Excel, vanwege de vaak complexe onderliggende berekeningen, bij uitstek geschikt.
Tussen de ruim 300 functies die Excel rijk is, zitten financiële functies waarmee u het beoordelen van investeringen kunnen vergemakkelijken.
Achtereenvolgens bekijken we in dit artikel de mogelijkheden van de functies.
HW (Rente, Aantal_termijnen, Bet, tw, type_getal)
NHW (rente;waarde1;waarde2; …)
IR (waarden;schatting)
NHW2 (rente;waarden;datums)
IR.SCHEMA (waarden;datums;schatting)
met als engelstalige tegenhangers
PV (Rente, Aantal_termijnen, Bet, tw, type_getal);
NPV(rente;waarde1;waarde2; …);
IRR(waarden;schatting);
XNPV(rente;waarden;datums);
XIRR (waarden;datums;schatting).
Met de functies HW, NHW en NHW2 kunt u de netto contante waarde bepalen, met de direct hieraan gelieerde functies IR en IR.SCHEMA, de interne rentabiliteit.
Om van alle genoemde functies gebruik te kunnen maken dient u vooraf de invoegtoepassing Analysis ToolPak te installeren. Deze is bereikbaar via de setupfunctie van Microsoft Excel of Office. De invoegtoepassing is te activeren via de menuoptie Extra – Invoegtoepassingen – Analysis ToolPak. Doet u dit niet, dan herkent Excel de functies niet en krijgt u de foutmelding #Naam
Voordat u aan de slag gaat met de verschillende functies geven we eerst nog een vijftal belangrijke tips en bekijken we de kenmerken van dynamische investeringsanalyses.
Vijf belangrijke tips bij investeringsanalyses
Bij het samenstellen van investeringsanalyses kunnen de volgende tips aan de hand worden gedaan:
1. Bepaal de tijdhorizon waarover het rendement moet worden berekend. Ga daarbij zoveel mogelijk uit van een reële levensduur van het investeringsobject en breng zo compleet mogelijk de inkomende en uitgaande kasstromen in beeld.
2. Bepaal of het een op zich staande investering betreft met onafhankelijke kasstromen of dat de investering ook invloed uitoefent op de staande organisatie en exploitatie. In het tweede geval dienen, voor een zuiver beeld, ook hiervan de exploitatiegevolgen meegenomen te worden in de vorm van kasstromen.
3. Bepaal een reële vermogenskostenvoet die zo goed mogelijk aansluit op uw financiële structuur en wensen. Een reële vermogens kostenvoet is gebaseerd op het WACC principe. De vermogenskostenvoet is bij investeringsanalyses gelijk aan de disconteringsvoet waarmee de kasstromen naar het investeringsmoment worden verdisconteerd.
4. Bepaal of aan het einde van het investeringsobject nog sprake is van een reële restwaarde. Kijk daarbij niet enkel door een boekhoudkundige bril maar vooral ook naar de economische levensduur en de te verwachten marktwaardeontwikkeling.
Dit laatste is vooral van belang bij investeringsanalyses op het gebied van onroerend goed.
5. Bepaal tot slot vooral ook “bandbreedtes” bij de vraag of u al of niet tot een investering besluit. Met die bandbreedtes, die kunnen liggen op het gebied van de kasstromen en / of de vermogenskostenvoet, kunt u verschillende varianten doorrekenen.
Dynamische investeringsanalyses: de kenmerken
Dynamische investeringsanalyses zijn altijd gebaseerd op de volgende uitgangspunten:
• Een tijdhorizon welke meerdere perioden omvat.
• Inkomsten en uitgavenstromen in plaats van kosten en opbrengsten.
• Er wordt rekening gehouden met de tijdwaarde van geld.
• Afschrijvingen blijven buiten beschouwing, het betreft namelijk geen uitgavenstroom.
• Rente blijft als uitgaven- of inkomstenstroom eveneens buiten beschouwing, maar het renteniveau worden wel meegenomen bij de bepaling van de hoogte van de disconteringsvoet die gebruikt wordt bij het contant maken van de verschillende stromen.
Bij het maken van dynamische investeringsberekeningen komen verder nog de volgende elementen om de hoek kijken:
De initiële investering
De initiële investering leidt op tijdstip “0” tot een eerste uitgaande stroom.
De kasstromen gedurende de exploitatie van de investering
Een investering leidt tot kasstromen. De aanschaf van een nieuwe machine kan bijvoorbeeld leiden tot een combinatie van lagere loon- en hogere energiekosten.
De (eventuele) Liquidatieopbrengst of restwaarde aan het einde van de looptijd
De verkoop van een investeringsobject, aan het einde van de investeringsperiode, levert restwaarde op. Betreft het de expiratie van financiële vermogenstitels dan geldt de eindaflossing als liquidatieopbrengst.
Tijdfactor en vermogenskostenvoet
Omdat een geldbedrag dat vandaag beschikbaar komt meer waarde heeft dan een gelijk bedrag in de toekomst, worden geldstromen contant gemaakt met de vermogenskostenvoet.
De vermogenskostenvoet wordt in principe door de investerende partij zelf bepaald. In de praktijk zal het percentage boven de kapitaalmarktrente liggen, plus een opslag voor het aan de investering verbonden risico.
De functie HW
Met behulp van de functie HW kunt u de contante of huidige waarde bepalen van kasstromen. Een nadeel van deze functie is dat alleen gewerkt kan worden met kasstromen van gelijke omvang. Ook biedt deze functie niet direct de mogelijkheid om de initiële investeringssom en de eventuele restwaarde op te nemen in de berekeningen.
De syntaxis van deze functie luidt als volgt:
HW (Rente, Aantal_termijnen, Bet, tw, type_getal)
waarbij de tussen haakjes staande argumenten de volgende betekenis hebben:
Rente: Het rentepercentage per termijn (moet dezelfde dimensie hebben als het argument “aantal termijnen”.
Aantal termijnen: Hier geeft u het totale aantal termijnen op.
Bet: Geeft het bedrag aan dat elke periode betaald of ontvangen wordt. Dit bedrag is voor elke periode gelijk.
tw: Dit is de toekomstige waarde. Als u het argument Bet gebruikt, dient u dit argument weg te laten (vice versa geldt het omgekeerde ook ).
type_getal: U geeft 1 aan als de betalingen telkens aan het begin van een periode voldaan worden. Als u 0 aangeeft (of dit argument leeg laat) betekent dit dat de betalingen telkens aan het eind van een periode voldaan worden.
Een voorbeeld
We berekenen de contante waarde van een investering groot € 5.000, welke gedurende 7 jaar een gelijkblijvende kasstroom te zien geeft van € 1.000. We gaan uit van een disconteringsvoet van 5,5% en er is geen restant waarde.
Volgens de regels van de financiële rekenkunde krijgen we bij dit voorbeeld de volgende vergelijking:
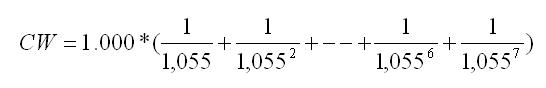
Als we gebruik maken van functie HW(rente;aantal-termijnen;bet;tw;type_getal) dan vullen we dit voorbeeld als volgt in:
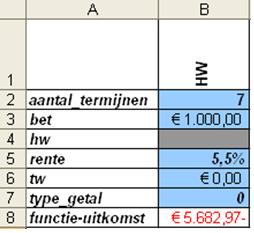
Invulling van de functieargumenten in de cellen B2 tot en met B7 leidt tot een contante waarde van € 5.682,97 in cel B8.
De stroom inkomende bedragen vertegenwoordigt dus een huidige waarde van € 5.682,97, waarmee de investering van € 5.000 als rendabel bestempeld kan worden. Er is in dit verband sprake van een overwaarde of rendabele top van € 682,97.
Indien we in het voorbeeld toch rekening willen houden met een restwaarde, dan moeten we hiervan de contante waarde afzonderlijk berekenen en de uitkomst bij het al berekende resultaat betrekken.
Als we bijvoorbeeld aannemen dat aan het einde van jaar 7 een waarde resteert van € 1.500 dan kunnen we met behulp van de functie HW ook hiervan de contante waarde bepalen.
De bijbehorende argumenten (dit keer laten we het argument “BET” leeg en gebruiken we het argument “TW” !) vullen we als volgt in:
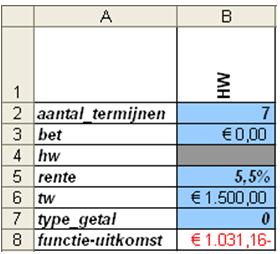
De restwaarde vertegenwoordigt een bedrag van € 1.031,16. Dit bedrag mag bij de oorspronkelijk overwaarde opgeteld worden, waarmee deze in totaal uitkomt
op € 1.718.60.
Met andere woorden: met het dubbel inzetten van de functie HW (voor de reguliere kasstromen en de restwaarde) kunt u een heel eind komen. Het grote manco van deze methode blijft echter dat u enkel met vaste kasstromen kunt werken. Dat zal in de praktijk zelden het geval zijn. Doorgaans komt dit alleen voor bij vastrentende vermogenstitels.
Bij in de tijd variërende kasstromen (dit kan zijn in de vorm van bedrag en / of voorlooptekens) kan, om de contante waarde en de interne rentabiliteit te meten,
beter gebruik maakt worden van de functies NHW en NHW2, respectievelijk IR en IR.SCHEMA,
De functies NHW en IR
Bij de berekening van de netto contante waarde en de interne rentabiliteit van wisselende kasstromen met een gelijk tijdsinterval, maken we gebruik van de functies
NHW(rente;waarde1;waarde2; …)
respectievelijk
IR(waarden;schatting)
Met de functie IR berekenen we de rentevoet waarvoor NHW gelijk is aan 0, ofwel NHW(IR(…); …) = 0.
Het is mogelijk om met zowel positieve als negatieve bedragen te werken.
De algemene vergelijking voor de berekening van de Netto contante waarde luidt:
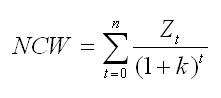
waarbij
• Z = de in- en uitgaande stromen van het investeringsproject;
• k = de vermogenskostenvoet;
• t = het aantal perioden.
Om tot de bepaling van de interne rentabiliteit te komen wordt aan deze vergelijking de waarde “0” toegekend:
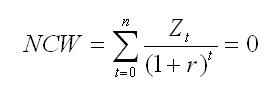
waarbij “r” berekend wordt als de interne rentabiliteit van het investeringsproject.
Op basis van het principe van de eerste vergelijking bepaalt NHW de netto contante waarde.
Op basis van de tweede vergelijking bepaalt IR vervolgens de bijbehorende interne rentabiliteit.
Van belang bij de functie NHW is, dat Excel ervan uitgaat dat de eerste cashflow pas aan het eind van de eerste termijn wordt ontvangen. Hiervoor moeten we een correctie doorvoeren in de berekening.
Een Voorbeeld
U overweegt een investering te doen van € 150.000. Deze investering leidt naar verwachting de daaropvolgende jaren (jaarlijks achteraf te beginnen bij jaar 1) tot inkomsten groot € 50.000, € 20.000, € 20.000, € 50.000, € 20.000, € 50.000 en € 20.000. Als het disconteringspercentage 8,5% op jaarbasis bedraagt, bereken dan met de functie NHW de huidige netto contante waarde van deze investering. Bereken vervolgens ook de interne rentabiliteit op basis van de functie IR.
Uitwerking: bepalen van de NCW
Na invulling van de opgegeven bedragen (cel B4 tot en met B11) en het rentepercentage (cel B1) krijgen we voor NHW een 'ongecorrigeerde' uitkomst van € 18.484,44 te zien in cel B13
B13 = NHW(B1;B4:B11)
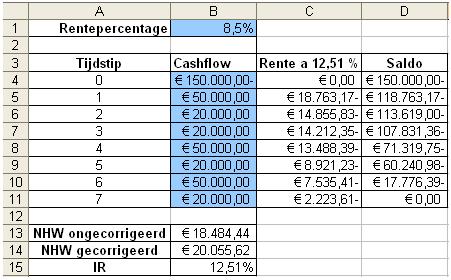
Omdat de investering al op tijdstip 0 plaatsvindt moeten we nog een correctie doorvoeren:
NHW(B1;B4:B11)*(1+B1) = € 18.484,44 * 1,085 = € 20.055,62
De aldus gecorrigeerde NHW van € 20.055,62 (B14) geeft tot slot de overwaarde of rendabele top aan van de investering bij het gewenste rendement van 8,5%.
Mocht de NHW daarentegen negatief uitvallen, dan is sprake van een onrendabele investering en wordt het gewenste rendement niet gehaald.
Uitwerking: bepalen van de IR
De interne rentabiliteit IR, waarmee de netto contante waarde precies op 0 uitkomt, bedraagt in dit voorbeeld 12,51%. Dit is het resultaat na invulling van de functie IR in cel B15.
B15 =IR(B4:B11;0)
De IR ligt in dit geval (aanzienlijk) boven het gewenste rendement van 8,5%.
Ter overweging en controle: als we het door de investeerder gewenste rendement zouden verhogen van 8,5% (cel B1) naar de gevonden 12,51%, komt de netto contante waarde weer (nagenoeg) op 0 uit!
De werking van de functies nader geïllustreerd
Uit de toegevoegde hulpkolommen C en D blijkt de rekenkundige werking van de functie IR. In kolom C wordt daartoe het uitstaande saldo van de vorige periode (kolom D) steeds vermenigvuldigd met de gevonden waarde voor de interne rentabiliteit (12,51%). Na de laatste inkomstenstroom resteert uiteindelijk precies een saldo van 0.
Uit deze analyse blijkt dat de functie IR impliciet drijft op twee cruciale veronderstellingen:
• er wordt rente verkregen op het aan het eind van elke periode uitstaande saldo;
• de in deze functie gehanteerde rentevoet (12,51%) blijkt voor positieve en negatieve saldi (stromen) gelijk te zijn.
De functies NHW2 en IR.SCHEMA
In het voorgaande zagen we dat we, voor de berekening van de netto contante waarde en de interne rentabiliteit van kasstromen met een gelijk tijdsinterval, gebruik kunnen maken van de functies NHW(rente;waarde1;waarde2; …) en IR(waarden;schatting).
Bij de berekening van de netto contante waarde en de interne rentabiliteit van kasstromen met een ongelijk en gedetailleerd tijdsinterval, kunnen we gebruik maken van de functies
NHW2(rente;waarden;datums)
en
IR.SCHEMA(waarden;datums;schatting).
Bij de weging en discontering van kasstromen gaan de functies NHW2 en IR.SCHEMA uit van een datumschema.
Een Voorbeeld
We sluiten voor het gemak aan op de bedragen van het eerdere voorbeeld, maar stellen nu, i.p.v. de (jaar)tijdstippen 0 tot en met 7, een gedetailleerd datumschema op.
De investering vindt plaats op 1 januari 2004, de daaropvolgende (positieve) kasstromen komen op verschillende data binnen in de daaropvolgende 6 jaren.
De functies vullen we daarbij als volgt in
B14 = NHW2(B2;B5:B12;A5:A12)
en
B15 = IR.SCHEMA(B5:B12;A5:A12)
We zien dat de uitkomsten in cel B14 respectievelijk B15 hoger liggen dan de eerder gevonden uitkomsten zoals berekend met de functies NHW en IR:
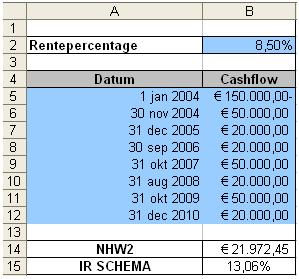
Het positieve verschil wordt veroorzaakt doordat de inkomsten nu gemiddeld vroeger in het jaar ontvangen worden.
De nauwkeurige wijze waarop de functie NHW2 met de ingevulde data omgaat is gestoeld op onderstaande vergelijking:
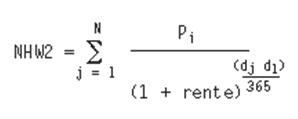
waarbij:
dj = je betaaldatum
d1 = 1e betaaldatum;
Pj = je betaling
Hierop aansluitend hanteert ook de functie IR.SCHEMA dezelfde mate van nauwkeurigheid:
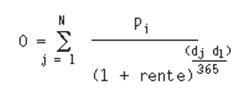
Tot slot: Wanneer gebruiken we welke functie?
In dit artikel hebben we de mogelijkheden van verschillende Excel functies getoond.
Met de functie HW kunnen we weliswaar de contante waarde van kasstromen bepalen, maar in de praktijk zal deze functie bij wat complexere investeringsanalyses al snel tekort schieten.
Willen we op globale basis een investeringsanalyse samenstellen dan komen we terecht bij de functies NHW en IR.
Komt het op uiterste (datum)nauwkeurigheid en “cijfers achter de komma” aan, dan is het gebruik van de functies NHW2 en IR.SCHEMA aan te bevelen.
_______________________________________________________________________________________
Klassiekers uit het archief van Financieel-Management.nl:
10 veel voorkomende fouten in Excel
10 veel voorkomende fouten in Excel – deel 2
Bekijk ook de inspirerende video's:
Excel Video #1: Winstmaximalisatie met de oplosser
Excel Video #2: Bekijk alle opties met 'wat-als' analyses
Excel Video #3: Overzicht in een handomdraai met een 'histogram'
Excel Video #4: Elimineer fouten met snijpuntoperatoren
Excel Video #5: Boek tijdswinst met draaitabellen
Excel Video #6: Foutloos vermenigvuldigen met 'Productmat'
Excel Video #7: Effectief Formules controleren
Excel Video #8: Optimale rooster- of werkplanning
Excel Video #9: Sneller rekenen met 'plakken speciaal'
Excel Video #10: Snel foutmeldingen opsporen en herstellen
Ontdek meer verbluffende en eenvoudige mogelijkheden van Excel:
Cursus Excel voor Financials
Cursus Interactieve Dashboards met Excel
Cursus Effectieve liquiditeitsprognoses met Excel
Cursus VBA Excel

















